Sources

L’idée la plus simple quand on parle de source est de supposer que les dislocations puissent émerger spontanément sous la forme de paires appelées dipôles à partir de boucles infinitésimales s’étendant sous l’effet de la contrainte (un peu comme les particules et anti-particules se créent spontanément par des fluctuations du vide).

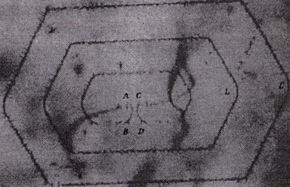
Source de F&R dans le silicium, remarquer les segments linéaires des boucles

En fait, pour qu’une boucle se développe, on montre qu’il faut fournir une contrainte supérieure à $\sigma=\mu b/r_c$, où $r_c$ est la taille critique de la boucle. Si le rayon des boucles est inférieur à $r_c$, elles disparaissent tout simplement (nous reparlerons de ce phénomène plus tard). En conclusion, les boucles de petits rayons ne contribuent pas à la plasticité. Il faut donc chercher dans des configurations particulières de dislocations qu’il faut chercher la solution. Nous venons de voir la source de Franck et Read. Elle se développe à partir d’un ancrage d’une dislocation sur deux segments sessiles.

Citons également deux autres exemples de sources (plus réalistes à mon sens) : la multiplication par glissement dévié et la multiplication par mécanisme de pôle.

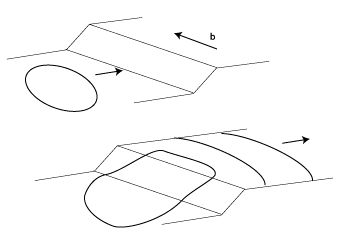
Nous avons vu précédemment que les segments vis pouvaient déviés dans un autre plan. Toutefois, une boucle de dislocation possédant des parties vis et coins ne peut se déplacer entièrement par ce processus à cause de la composante coin. Il s’ensuit alors qu’une partie de la boucle se trouve épingler et pouvant donc donner naissance à de nouvelles dislocations vis.

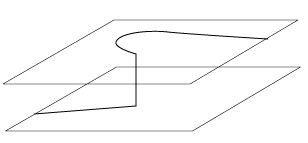
Dans le mécanisme de pôle, un point d’épinglage sessile sur une dislocation permet la croissance de belles boucles dites ouvertes à partir des segments glissiles.

La figure suivante illustre ce processus en montrant un segment épinglé sur un point P qui se multiplie en formant un second segment.

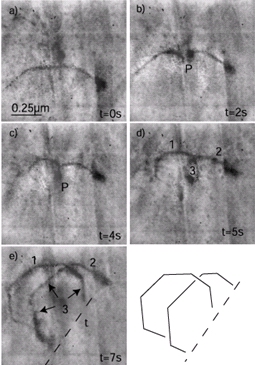
Source dans Al-Pd-Mn, cliché CEMES