Cristaux et Quasi-cristaux

Un quasi-cristal est un solide possédant un spectre de diffraction essentiellement discret selon l'union internationale de cristallographie... Si les cristaux sont courants (métaux et alliages, minéraux, céramiques, glace, sels...), il n'en est pas de même des quasi-cristaux, dont la découverte dans les années 1980 a mis fin à 200 ans de certitudes sur l'organisation de la matière cristalline.

Ordre, symétries et cristaux

L'observation des cristaux est loin d'être récente. Déjà les Égyptiens connaissaient la turquoise et les gemmes (diamant, saphir, émeraude, rubis) étaient très appréciés au temps de l'antiquité. En 64 avant JC, Strabo, invente le mot "Krystallos" pour désigner le quartz. Il est évident que les cristaux ont toujours fasciné tant par leur aspect translucide et coloré que par leur forme facettée. Ces deux aspects sont intimement liés aux propriétés physiques propres aux cristaux et au fait qu'ils soient ordonnés. Cependant cet ordre est resté fort longtemps incompris. L'histoire de la cristallographie s'étale principalement sur 2 siècles (19ème et 20ème siècles).

À partir de la fin du18ème, l'approche que l'on va avoir du monde des cristaux va être d'ordre purement géométrique, inspirée en cela par l'extrême rigidité du monde minéral. Domaine réservé tout d'abord aux naturalistes, la cristallographie va prendre son envol en France essentiellement au cours des 19 et 20ème siècles et sera marquée principalement par trois figures : Jean Baptiste Romé de L'Isle, René Just Hauy et Auguste Bravais.

Romé de l'Isle, en reprenant les travaux de Stenon, remarque en 1772 que, bien que les faces des cristaux soient en général de tailles différentes du fait même de leur croissance, deux faces adjacentes forment toujours entre elles des angles égaux. Cette loi tout à fait générale ouvre la voie à une description unique de l'ensemble des cristaux en termes purement géométriques. Cependant il n'arrivera pas à déterminer l'ensemble des formes à partir de ce principe unique.

C'est l'abbé René Just Hauy qui va réaliser le bond en avant et ceci par une découverte fortuite ! En faisant tomber un cristal de calcite, il découvre qu'en se brisant, les fragments de tailles différentes présentent toujours le même caractère de facette que le cristal d'origine. Hauy en déduit que le cristal d'origine peut être décrit par un empilement de "molécules" semblables qu'il nomme "molécule intégrante". Celles-ci, de forme parallélépipédique, s'emboîtent parfaitement pour constituer un solide homogène. D'après ce principe, la forme d'un cristal va dépendre du nombre d'éléments le composant, de sorte que les faces du cristal soient formées de minuscules gradins. En effectuant ainsi ce qu'il appelle le "décroissement égal sur tous les sommets", et qui consiste simplement à enlever des parallélépipèdes en nombre décroissant à partir des sommets ou d'une arête de la forme complète, il explique un grand nombre de formes naturelles (par exemple à partir d'un cube, on peut par décroissement à partir des sommets obtenir une morphologie octaèdrique, comme par exemple celle de la fluorine). Il retrouve ainsi la loi de Romé de L'Isle sur la constance des angles puisque pour un empilement les angles sont conservés, et explique du même coup la notion de clivage.

Son travail ne s'arrête pas la puisqu'il trouve de façon mathématique que beaucoup de formes idealisées peuvent être décrites par 3 types de parallelepipèdes, dits primitifs. Du meme coup, il montre l'impossibilité de construire un cristal avec des prismes pentagonaux, octogonaux... C'est le triomphe de l'esprit geométrique ! Delafosse, élève d'Hauy remplacera le terme de molécule intégrante par celui de "maille élémentaire" , terme qui restera à la postérité. Cependant, les déductions d'Hauy ne sont pas complètes pour décrire l'ensemble des structures cristallographiques. Ceci nous amène à la definition du cristal (plus précisement du reseau cristallin) comme étant la répétition (ou si on préfère l'empilement) d'une maille élémentaire dans les trois directions de l'espace: un cristal est un objet "périodique".

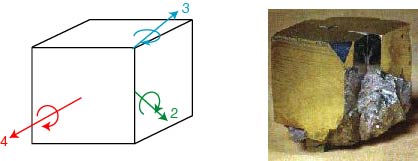
Les travaux d'Hauy vont être repris par Weiss lequel va recenser les faces d'un cristal par rapport a des éléments de symétrie. Ce principe très puissant dans le monde de la physique va guider toute la cristallographie. Ainsi, pour passer d'une face a l'autre, on doit appliquer une opération de symétrie qui peut être une rotation, une inversion par rapport a un centre... Si on prend une morphologie cubique (comme la pyrite), il est facile de voir les axes de symétrie de rotation : un axe d'ordre 3 sur les sommets, un axe d'ordre 2 sur les arrêtes, d'ordre 4 sur les faces (un axe de rotation est dit d'ordre $n$ lorsqu'il y a invariance après une rotation de $2\pi /n$ autour de l'axe).

C'est là que Auguste Bravais entre en scène. En 1848, il rend une étude purement mathématique sur la classification des cristaux. Il décrit l'ensemble des structures possédant des symétries d'orientation compatibles avec la triple périodicité des cristaux dans les trois directions de l'espace (symétrie de translation). Il trouve ainsi 32 classes de symétrie réparties en 14 types de réseaux (réseaux de Bravais) que l'on peut regrouper en 7 systèmes définissant la forme de la maille élémentaire. De 3, on est passé à 7 mailles ! Cette analyse nous dit simplement que l'on ne peut disposer les points d'un réseau de façon arbitraire. Prenons le cas plus simple d'un réseau du plan (les résultats se généralisent à 3D).

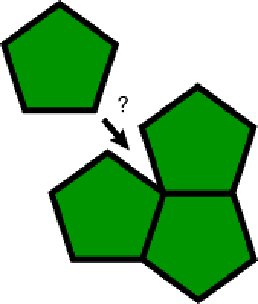
Partons de la plus petite distance, $d$, entre deux nœuds du réseau. Une rotation d'angle $\theta$ du réseau conduit a deux nouveaux nœuds qui doivent se superposer à des nœuds du réseau pour que la rotation soit une opération de symétrie. Une rapide analyse géométrique conduit à la conclusion suivante: le réseau reste invariant seulement pour des valeurs particulières de $\theta$ . En d'autres termes les rotations d'ordre 1, 2, 3, 4 et 6 sont les seules permises. Il n'existe pas de cristal avec d'axe de symétrie d'ordre 5, pour la même raison qu'il n'y pas de dallage ou de tapisserie avec des pentagones.

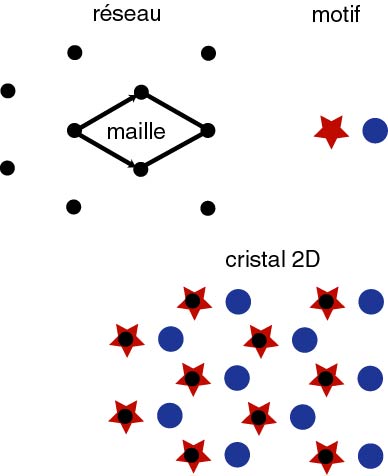
L'histoire est cependant loin d'être finie. L'ère purement géométrique venait de finir, elle avait permis la classification exhaustive de l'ensemble des structures, reste à savoir ce qu'était véritablement une structure réelle. En cette fin de 19ème siècle, la physique est en ébullition tant le concept d'atome bouleverse les règles établies. La théorie atomiste naissante est en partie bâtie à partir des conclusions fournies par la cristallographie. Delafosse en introduisant le concept de maille avait déjà pressenti que l'on pouvait dissocier organisation et composant élémentaire: le cristal peut être décrit par une maille élémentaire décorée par un motif atomique.

La découverte de la nature réticulaire des cristaux, c'est-à-dire le fait que l'on puisse décrire les structures comme un ensemble de familles de plans (un empilement de couches d'atomes), chaque plan d'une même famille étant séparé d'une distance constante (distance inter-réticulaire), va entrainer une petite révolution. Elle est due à Max Von Laue (prix Nobel 1914) qui découvre que les rayons X sont diffractés par la matière cristalline. En simplifiant, on peut dire que ce phénomène est analogue a celui que l'on rencontre lorsque l'on regarde un réverbère à travers un store. La lumière est dispersée. Ce phénomène se rencontre à chaque fois que la taille de la fente par laquelle on fait traverser un rayonnement est de l'ordre de la longueur d'onde (analogue à la distance entre deux crètes d'une vague). Pour un cristal, la distance entre deux plans est de l'ordre de la distance entre atomes, ce qui est vraiment petit : 1/10 de milliardième de mètre (1000 fois plus petit que l'épaisseur d'un cheveu). Dans ce cas pour obtenir le phénomène de diffraction, il faut un rayonnement dont la longueur d'onde est très courte. Cette condition est réalisée par les rayons X et c'est grâce à eux que l'on peut sonder la matière ! En particulier lorsqu'on éclaire un cristal dans une orientation particulière, le rayonnement n'est diffracté que dans des directions spécifiques: on obtient des clichés dits de diffraction, un réseau de tâches qui a le bon goût d'avoir les mêmes symétries que le cristal...

Le travail de caractérisation des structures cristallines fut alors engagé par les Bragg père et fils (prix Nobel 1915) et ne cessa de se développer avec un grand succès.

On a ainsi identifie un grand nombre de structures. Par exemple, les métaux cristallisent selon trois types de réseaux: cubique centre (fer, chrome), cubique faces centrées (aluminium, cuivre), et hexagonal (zinc, titane). D'autres structures cristallisent aussi. C'est par exemple les protéines, les virus... L'exemple reste le plus célèbre est celui de la molécule d'ADN, constituant élémentaire de nos cellules. En 1953, Crick et Watson découvrent la structure en double hélice de cette molécule grâce à l'analyse des clichés de diffraction réalisés dans l'ombre par R. Franklin de la molécule cristallisée.

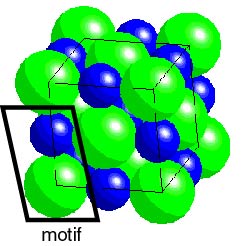
Le sel de mer est lui aussi un cristal: celui de chlorure de sodium (NaCl) qui cristallise selon un réseau cubique faces centrées. Dans ce cas on comprend mieux la notion de maille et de motif atomique décorant la maille. Un atome de chlore (vert) et un atome de sodium (bleu) forment le motif élémentaire qui se retrouve aux sommets et aux centres des faces d'un cube élémentaire.

Quasi-cristaux et symétries interdites

Imaginez vous maintenant dans la peau de Dan Shechtman, un chercheur israélien invité au National Bureau of Standard (NBS) aux états unis en 1982, lorsqu'en travaillant sur un alliage d'aluminium et de manganèse rapidement solidifié, il observât un cliché de diffraction de symétrie pentagonale.

Zn-Mg-Ho diffraction from Wikipedia

Les alliages trempes (refroidis très rapidement) de Shechtman, n'étaient pas des cas idéaux de quasi-cristaux, et bien des polémiques voulurent les faire passer pour des cristaux qui imiteraient des symétries interdites... la face du monde en aurait été sauvée. Au rang des détracteurs, on note même la présence du double prix Nobel, Linus Pauling. Cependant la cristallographie "traditionnelle" ne put être sauvée : les quasi-cristaux étaient bien une réalité. Outre Shechtman, qui recevra le prix Nobel de Chimie 2011, trois autres chercheurs doivent être associés à cette découverte (ils signent l'article fondateur des quasi-cristaux de 1984): I. Blech lui aussi chercheur au Technion de Haïfa, J. W. Cahn, un américain du NBS (aujourd'hui le NIST), et un français Denis Gratias, chercheur au CECM (aujourd'hui à l'école de chimie de Paris). Bien que cette nouvelle soit une des découvertes majeures du 20ème siècle, elle n'étonna en rien les mathématiciens qui connaissaient déjà les objets non-périodiques.

En effet le cadre mathématique dans lequel allait s'inscrire cette découverte, n'était pas nouveau. Il s'appuie en particulier sur les travaux de H. Bohr et A. Besicovic sur les "fonctions presque-périodiques" et datant des années 30, sans oublier le travail plus récent de R. Penrose sur les pavages non-périodiques (1974) qui resteront les archétypes des quasi-cristaux. Ces pavages bien que non périodiques, sont construits à partir de 2 tuiles selon des règles strictes d'accolement qui les rend parfaitement ordonnés et présentent une symétrie d'ordre 5 (du moins d'un point de vue local).

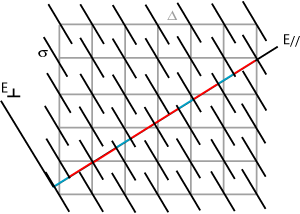
L'année même de la découverte (1984), P. Steinhardt et D. Levine donnent une première interprétation géométrique et fondent le terme de "quasi-cristal". En 1985 A. Katz et M. Duneau de l'école Polytechnique donnent une description des quasi-cristaux en terme de cristallographie dans un espace à plusieurs dimensions. Ces structures résultent alors de la "coupe irrationnelle" de cet espace périodique. Pour illustrer le concept, prenons l'exemple simple d'un "quasi-cristal" a 1D. Pour cela d'un réseau carré à deux dimensions dans lequel on a place des petits segments sur les nœuds (et dont la taille est astucieusement choisie). Maintenant on coupe ce réseau avec une droite dont la pente est irrationnelle. Lorsque cette pente est égale à l'inverse du nombre d'or, on obtient une série de segments courts et longs qui suivent la séquence non périodique de Fibonnacci. De la même facon un pavage de Penrose peut être construit par la coupe irrationnelle d'un espace à 4 dimensions. Les quasi-cristaux de Dan Schechtman nécessitent une description dans un espace périodique à 6 dimensions.

L'année suivante, cette description est définitivement adoptée après les travaux des russes Kitaev, Levitov et Kalugin et de l'américain Elser. A partir de là, on arrive à reconstituer les fameux diagrammes de diffraction de D. Shechtman.

On pensait alors que le seul problème résidait dans la croissance de quasi-cristaux de bonne taille et de bonne qualité. C'est alors que L. Bendersky découvrit des phases de symétrie décagonale. Ces phases ont une structure quasi-périodique à deux dimensions, la troisième dimension étant périodique. S'ensuivit jusqu'à aujourd'hui la découverte d'une centaine de phases dont les plus étudiées : les alliages ternaires aluminium, palladium, manganèse (Al-Pd-Mn) et aluminium cuivre fer (Al-Cu-Fe). Lorsque l'on refroidit un mélange en fusion d'aluminium, palladium et manganèse en quantité précise (70% Al, 20% Pd, 10% Mn), il est possible d'obtenir de beaux quasi-cristaux de taille macroscopique montrant des facettes pentagonales.

Dans les années 90, on perça le secret des structures réelles en terme de positions atomiques dont la redoutable complexité laisse de nombreuses questions ouvertes. Pour illustrer ceci, reprenons l'exemple de la coupe à 2 dimensions. Les petits segments attachés aux nœuds du réseau sont appelés surfaces atomiques. En première approximation, on peut les considérer comme des sphères dont les couches concentriques correspondent a des éléments chimiques différents. La figure ci-dessous représentent une vue en coupe a 2D du réseau 6D hypercubique faces centrées de Al-Pd-Mn quasicristallin. On retrouve les segments attachés aux nœuds (ici n, n' et bc) du réseau. Leur intersection avec l'espace "réel" correspond a la position et la nature des atomes. La taille et la forme des surfaces atomiques sont ajustées afin d'éviter des distances atomiques trop petites, une densité et une composition en accord avec les données expérimentales. Dans l'espace "réel", on s'est aperçu que 90% des atomes s'agrégeaient pour former des "amas" qui s'interpénètrent pour former la symétrie de l'icosaèdre.

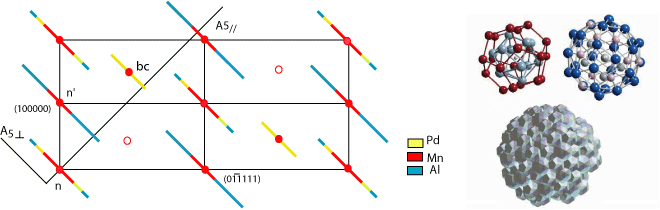
d'après D. Gratias

Les principales interrogations restent liées à l'origine de la stabilité de ces structures et de leur mode de croissance. Pensez par exemple que pour assembler un pavage de Penrose en ajoutant tuile à tuile, il est nécessaire de connaître la configuration de l'ensemble du pavage pour ne pas se planter... quel démon "shechtmannien" y-a-t-il derrière ?

Notons pour finir que l'étude des quasi-cristaux s'étend sur tous les domaines de la physique tant le caractère atypique de ces structures a une large incidence sur ses différentes propriétés physiques. On peut citer en particulier ses qualités d'isolant thermique et électrique bien que ce soit des alliages metalliques. Du point de vue de ses propriétés mécaniques, ils sont extrêmement fragiles et durs. Ceci leur confère d'excellentes qualités tribologiques, c'est a dire d'usure aux frottements. Ainsi on peut les imaginer rentrant dans la composition de certains revêtements (ce qui a été réalisé dans le cas d'une poêle anti-adhésive) ou en tant qu'isolant thermique.

Haut