Propriétés des dislocations¶

La dislocation est la solution qui est apparue aux physiciens pour localiser la déformation et de la rendre économique. Elles ont été déjà envisagées dans les milieux continus par le mathématicien Volterra (1907) et observées dans les cristaux liquides au début du 20ème siècle par G. Friedel.

La dislocation est un « objet » linéaire. Les deux paramètres importants d’une dislocation sont le pas de déplacement que l’on appelle le vecteur de Burgers et la ligne de discontinuité.

Commençons par voir à quoi correspond le vecteur de Burgers. Reprenons pour cela l’image classique de la dislocation vue perpendiculairement à la direction de la ligne (il s’agit ici d’une dislocation rectiligne un peu particulière comme on le verra dans la suite).

Pour caractériser le vecteur de Burgers d’une dislocation, on est conduit à observer la différence existant entre un tracé fermé dans une portion de cristal parfait et le même tracé dans la même portion du cristal contenant une dislocation.

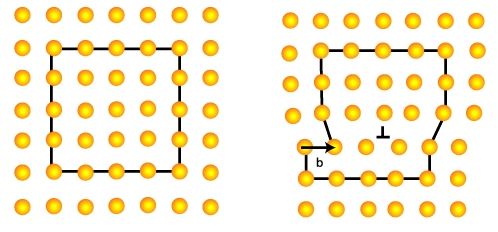
Dans le cristal parfait, un circuit fermé est obtenu en se déplaçant par sauts successifs égaux à une distance interatomique. Dans le cristal fauté, le même circuit (c'est-à-dire le même nombre de « sauts » dans chaque direction) ne se referme pas. Le vecteur manquant, qui est une translation du réseau, est appelé vecteur de Burgers.

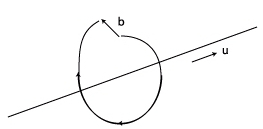
En terme plus mathématique, il traduit l’intégrale du déplacement autour d’un circuit fermé autour de la ligne, caractérisée par le vecteur $\vec{u}$ .

$\vec{b}=\oint d\vec{u}$

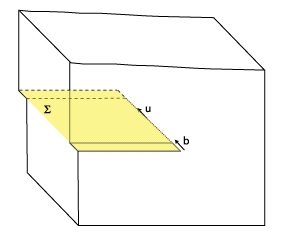
Pour caractériser la ligne de dislocation, il est intéressant d’étudier leur construction par le processus dit de Volterra. Considérons pour cela un solide homogène que nous découpons selon une surface quelconque. On crée alors deux lèvres de coupure. On peut alors déplacer ces deux lèvres l’une par rapport à l’autre d’une quantité égale au vecteur de Burgers, ajoutant ou retirant de la matière si nécessaire. En recollant les deux lèvres, on obtient de nouveau un solide homogène, mais cette fois, on a créé une ligne de singularité élastique appelée ligne de dislocation. Cette ligne est orientée par un vecteur $\vec{u}$ tangent à sa trajectoire (ceci permet de prendre une convention pour choisir le vecteur de Burgers).

En réalité pour éviter les divergences des contraintes élastiques engendrées par cette singularité, on considère que dans un petit rayon autour de la ligne les lois de l’élasticité ne s’appliquent plus. La description de cette zone, appelée le cœur de la dislocation requiert alors une analyse atomistique fine (nous verrons plus tard l’importance du cœur d’une dislocation en plasticité).

Dressons avant d’aller plus loin les caractéristiques importantes d’une dislocation :

une dislocation est complètement caractérisée par son vecteur de Burgers et la direction de sa ligne.
une dislocation étant une singularité élastique, ne peut se terminer dans le cristal parfait ; soit elle émerge en surface, soit elle forme une boucle.
le vecteur de Burgers est constant sur toute la ligne de dislocation.
la surface engendrée par la ligne de dislocation et son vecteur de Burgers est la surface de glissement. La dislocation peut se déplacer sur cette surface sans transport de matière.
le glissement correspond à la propagation d’un cisaillement élémentaire d’amplitude $\| \vec{b} \|$ . La dislocation correspond alors en quelque sorte un « quantum de déformation ».

Pour l’instant, nous avons parlé de considérations très générales. Parlons maintenant de deux types de dislocations élémentaires : la dislocation coin et la dislocation vis

Reprenons la construction de Volterra. Supposons pour simplifier que la surface de coupure $\Sigma$ soit un plan délimité par une ligne de dislocation rectiligne de vecteur $\vec{u}$ . Lorsque $\Sigma$ est déplacée selon la direction $\vec{b}_1$ parallèlement à $\vec{u}$ , on obtient une dislocation vis. Une dislocation coin est obtenue si $\vec{b}_2$ est perpendiculaire à $\vec{u}$ .

La dislocation vis¶

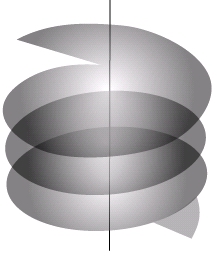
Pour bien comprendre ce qu’est véritablement une dislocation vis, il est intéressant de remarquer que le vecteur de Burgers d’une dislocation vis correspond dans le cristal, à la distance d’empilement des plans atomiques le long de la ligne de dislocation. La topologie de la dislocation vis correspond alors à une hélice : un point sur le « plan » atomique perpendiculaire à la ligne de dislocation monte d’un pas égal à $\| \vec{b} \|$ à chaque tour d’une trajectoire qui enroule la dislocation. Les plans ne forment plus qu’une seule surface comme un escalier en colimaçon, d’où le nom de dislocation vis.

La dislocation coin¶

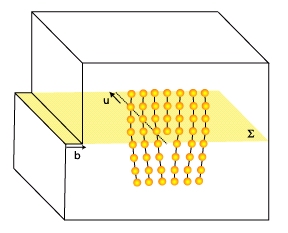
C’est la dislocation que l’on se représente le plus simplement. On peut la considérer comme le résultat de l’insertion de ce demi plan ce qui est analogue à un coin enfoncé dans une pièce de bois, d’où l’origine de son nom. Il est assez facile de voir que cette dislocation entraîne la compression de la partie supérieure du cristal et la compression de la partie inférieure. Nous reviendrons plus tard sur ce point.

Que se passe- t’il lorsque la dislocation est une boucle comme dans le cas général ? Certaines portions seront coins et d’autres vis. Lorsque le vecteur de Burgers forme un angle quelconque avec la ligne de dislocation, on dit que son caractère est mixte.

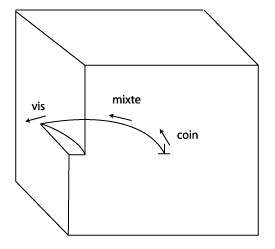
Ainsi une boucle de dislocation polygonale (on verra plus tard que dans certains cristaux, les dislocations préfèrent se mettre dans des directions particulières) ayant un vecteur de Burgers dans son plan peut avoir des segments de caractère différent. On verra également plus tard que la mobilité d’une dislocation dépend du caractère de la dislocation.