L'Enigme de la Plasticité des Métaux

Ce texte a été publié dans le Bulletin de l'Union des Physiciens (BUP), n°879, 2005

Rien de plus banal que de tordre une petite cuillère ou un fil de cuivre. Cette capacité des matériaux à se déformer de façon irréversible, appelée « plasticité » est extrêmement importante en métallurgie dans les opérations de mise en forme (forgeage, laminage, tréfilage…). Plus important encore est le fait que la plasticité donne aux matériaux leur résistance à se déformer sans se rompre comme le font les matériaux fragiles. Pourtant, il a fallu seulement attendre les années 1930 pour comprendre de façon théorique les mécanismes élémentaires de plasticité en introduisant le concept de dislocation, et seulement les années 1950 pour observer ces étranges objets. Dans cet article, on verra en quoi les dislocations sont nécessaires pour expliquer la déformation plastique, puis on s’attardera ensuite sur leur description en terme géométrique. On verra également que les dislocations possèdent un champ de contrainte à longue distance qui leur permet d’interagir entre elles et avec une contrainte extérieure. Enfin, on montrera brièvement comment les mécanismes impliquant le mouvement des dislocations expliquent les performances mécaniques des métaux et de leurs alliages.

Déformation élastique et déformation plastique

Au début de la déformation d’une éprouvette, les liaisons entre les atomes commencent par se « distendre », à la manière d’un ressort, de sorte que le relâchement de la contrainte rétablit la forme initiale de l’éprouvette. La courbe de la contrainte (force ramenée à la surface de la section de l’éprouvette) en fonction de la déformation (pourcentage d’allongement dans la direction de traction) est linéaire et réversible : c’est la loi de Hooke.

Figure 1: Courbe typique de contrainte ($\sigma$) en fonction de la déformation ($\epsilon$) pour une éprouvette métallique étirée à vitesse constante

On parle de déformation élastique. Au-delà de la limite d’élasticité (en général plusieurs tonnes par cm²), les matériaux ductiles (par opposition à fragiles) continuent de se déformer, mais la contrainte croît moins vite pour assurer une vitesse de déformation constante. Cependant, cette déformation n’est pas réversible et un allongement résiduel subsiste après la suppression de la contrainte. On parle de déformation plastique. Toutefois, comme la décharge de l’éprouvette s’effectue réversiblement, la limite d’élasticité augmente lors d’une nouvelle déformation. Le matériau s’est durci. En d’autres termes, le matériau ayant gardé la mémoire d’une première déformation est capable de supporter une contrainte plus grande la seconde fois avant de se déformer plastiquement. Ce phénomène appelé écrouissage était bien connu des forgerons qui avaient compris l’intérêt du martelage des métaux pour augmenter leur résistance.

Le paradoxe de la déformation des métaux

Il est clair que la déformation plastique nécessite un réarrangement important de la matière. Pourtant, cette situation semble paradoxale dans les métaux, où la structure interne (celle d’un cristal où les atomes sont répartis sur un réseau périodique tridimensionnel) doit être conservée malgré les changements de forme extérieure. La façon la plus intuitive d’imaginer la déformation est de considérer qu’elle procède par une série de glissements élémentaires le long de plans atomiques, à la manière des feuilles d’une rame de papier qui glissent les unes sur les autres.

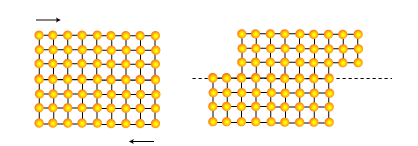
Figure 2 : Représentation schématique en coupe d’un cisaillement dans un matériau cristallin.

Partons du cas le plus simple d’un cristal cubique simple, et déplaçons en cisaillement la partie supérieure de la quantité ''x'' par rapport à la partie inférieure. Pour effectuer un tel déplacement, il est nécessaire d’amener les atomes de la partie supérieure en contact avec ceux de la partie inférieure dans une position instable. On peut imaginer ce phénomène par l’image simplifiée d’une bille roulant sur une tôle ondulée.

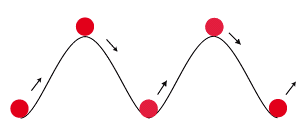
Figure 3

En terme mathématique, on exprime la contrainte nécessaire pour déplacer un atome dans ce potentiel par une fonction périodique et qui est minimale chaque fois que l’on s’est déplacé d’une distance interatomique dans le sens du mouvement :

$$\tau(x)=\mu K \sin{\left( 2\pi\frac{x}{b} \right)}$$

$\mu$ (le module de cisaillement) étant une constante mesurant l’aptitude d’un matériau au cisaillement. Il est typiquement de l’ordre de la centaine de tonnes par cm² . En supposant pour les petits déplacements que la déformation est élastique, on peut écrire ( cf. figure 4) :

$$\tau(x)=\mu \frac{x}{a}$$

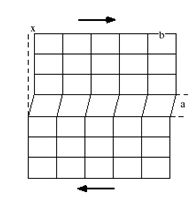
Figure 4

On obtient finalement :

$$\tau(x)=\frac{\mu b}{2\pi a} \sin{\left( 2\pi\frac{x}{b} \right)}$$

La valeur maximum de cette contrainte est alors $\tau=0.2 \mu$ soit mille à dix mille fois plus que la valeur expérimentale ! Si la déformation était purement élastique, on pourrait suspendre une automobile à un fil cylindrique d’aluminium de 1 mm de rayon !

L'énigme résolue

Dans les années 1930, Orowan, Polanyi et Taylor proposèrent que le cisaillement pût se produire par la propagation de défauts linéaires élémentaires appelés dislocations. Supposons qu’un cisaillement élémentaire d’une distance interatomique $\vec{b}$ se produise uniquement le long d’une partie du plan de cisaillement. La ligne qui sépare la partie qui a été cisaillée de celle qui ne l’est pas, est la ligne de dislocation. Elle apparaît ici comme la limite d’un demi-plan atomique qui distord fortement les plans voisins.

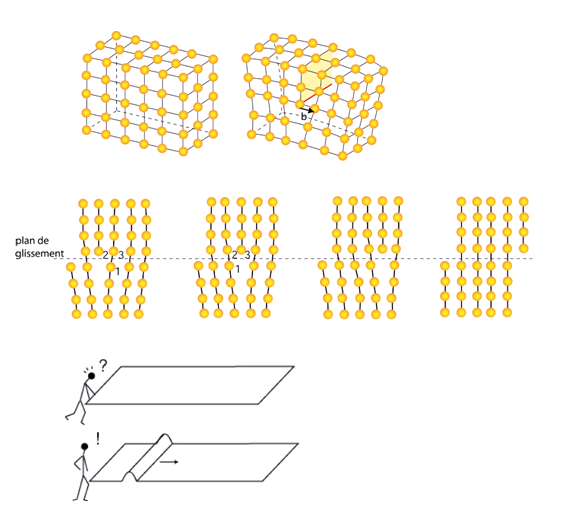
Figure 5

Il est facile de voir que cette dislocation peut se propager d’une surface du cristal à l’autre en coupant et recollant de proche en proche les liaisons atomiques, à la manière d’une double fermeture éclair. Par analogie, déplacer un tapis sur le sol est beaucoup plus facile si on fait propager une petite bosse d’un bout à l’autre.

Ces étranges objets

Une dislocation est un « objet » linéaire caractérisé par une ligne de discontinuité $\vec{u}$ et un pas de déplacement, appelé le vecteur de Burgers $\vec{b}$. Ce dernier représente le vecteur nécessaire à boucler un circuit initialement fermé dans le cristal et qui se trouve ouvert lorsqu’il enlace la dislocation ( il s’agit de l’intégral de déplacement autour d’un circuit fermé autour de la dislocation).

Leur construction formelle dans un milieu élastique et continu peut être décrite par le processus de Volterra. Considérons pour cela un solide homogène que nous découpons selon une surface quelconque. On crée alors deux lèvres de coupure que l’on peut alors déplacer l’une par rapport à l’autre d’une quantité égale au vecteur de Burgers, ajoutant ou retirant de la matière si nécessaire. Dans un matériau cristallin, ce vecteur n’est pas quelconque, mais représente une translation du réseau. En recollant les deux lèvres, on obtient de nouveau un solide homogène, mais cette fois, on a créé une ligne de singularité élastique appelée ligne de dislocation. Cette ligne est orientée par un vecteur $\vec{u}$ tangent à sa trajectoire (ceci permet de prendre une convention pour choisir le vecteur de Burgers).

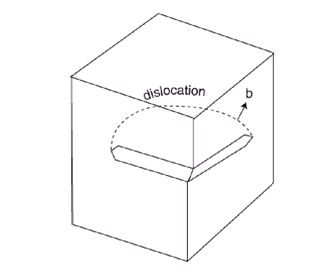
Figure 6

Deux cas particuliers de dislocations se distinguent : la dislocation coin ($\vec{u} \perp \vec{b}$) et la dislocation vis ($\vec{u} \| \vec{b}$). Une dislocation dite coin peut être vue comme le résultat de l’insertion d’un demi-plan atomique dans la structure, à la manière dont on enfoncerait un coin dans une pièce de bois. La dislocation vis tire son nom du fait que chaque point sur le « plan » atomique perpendiculaire à la ligne de dislocation monte d’un pas égal à $\| \vec{b}\|$ à chaque tour d’une trajectoire qui enroule la dislocation. La topologie du champ de contrainte autour de la dislocation est donc celle d’une hélice. Dans les autres cas, on dit que la dislocation a un caractère mixte.

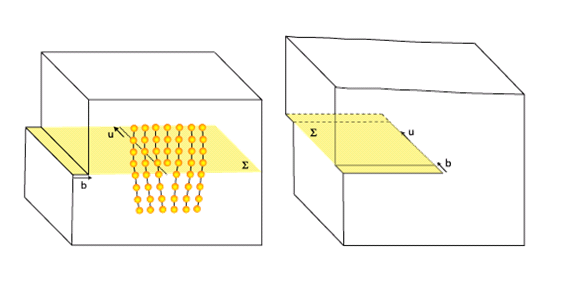
Figure 7

Les dislocations isolées, étant des singularités élastiques, développent autour d’elle un champ élastique à longue distance de portée infinie, comme un électron est entouré d’un champ électromagnétique. Dans le cas de la dislocation vis, il a une symétrie cylindrique de la forme:

$$\sigma= \frac{\mu b}{2 \pi r}$$

On voit qu’il est proportionnel au vecteur de Burgers (ce qui est analogue à la charge électrique), au module de cisaillement (analogue à la permittivité électrique du milieu), et inversement proportionnelle à la distance. Ainsi, une dislocation peut être vue comme un quantum de déformation élémentaire. Comme les dislocations possèdent un champ élastique, elles peuvent interagir avec un champ extérieur ou avec le champ d’autres dislocations. Considérons ainsi, de manière simplifiée, une dislocation traversant complètement un échantillon de dimension $L$ sur $l$ sous l’influence d’une contrainte extérieure de cisaillement $\tau$.

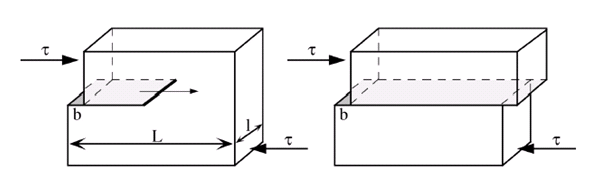
Figure 8

En traversant l’échantillon, les deux parties de l’échantillon ont été déplacées d’une quantité $b$. Le travail $W$ de la force appliquée $F$ sur l’échantillon est donc :

$$W_C=F_C b=\tau (Ll) b$$

Ce travail est égal à celui de la force $F$ nécessaire pour déplacer la dislocation de longueur $l$ sur la distance $L$, et qui s’écrit :

$$W=FL$$

En réalité il s’agit du tenseur de contrainte dont les seules composantes non nulles correspondent à des cisaillements purs dans les plans radiaux parallèles à $\vec{u}$ et dans les plans horizontaux perpendiculaires à un rayon autour de la dislocation.

Ceci nous conduit alors à l’expression de la force (par unité de longueur) exercée sur une dislocation par une contrainte extérieure :

$$\frac{F}{l}=\tau b$$

Prenons maintenant comme exemple deux dislocations vis parallèles séparées d’une distance $R$. La force subie par la dislocation de vecteur $\vec{b}_1$ dans le champ de contrainte de la seconde (de la forme $\sigma=\mu b_2/R$) est alors :

$$\vec{F}= \frac{\mu \vec{b}_1 \vec{b}_2}{2 \pi R^2} \vec{R}$$

Cette force est radiale et décroissante en $1/R$ (elle ne dépend que de la distance entre les dislocations). Elle est attractive si les vecteurs de Burgers sont opposés et répulsive dans le cas contraire. Il n’est ainsi pas rare par exemple de voir deux dislocations s’annihiler comme le feraient un électron et un positron.

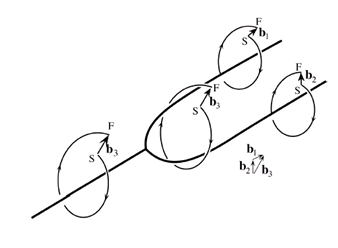
Figure 9

Cependant, l’analogie s’arrête là, car les dislocations sont des objets flexibles et la déformation qu’elles transportent est une grandeur vectorielle. Ceci a deux conséquences importantes. D’une part, deux dislocations peuvent interagir entre elles pour en former une troisième : on parle alors de jonction attractive. Dans ce processus, la quantité de déformation est conservée. Il s’ensuit qu’à un nœud entre plusieurs dislocations, la somme des vecteurs de Burgers est nulle (ceci est analogue à la loi de Kirchhoff).

D’autre part, comme elles possèdent une énergie élastique proportionnelle à leur longueur, les dislocations ont tendance à se comporter comme la corde d’un arc, résistant à tout allongement ou courbure. Pour une dislocation vis rectiligne, le travail effectué pour déplacer les deux parties du cristal d’une distance $b$ est donné par :

$$E=\frac{1}{2} \int_{r_0}^R \tau b dr = \frac{1}{2} \int_{r_0}^R \frac{\mu b}{2 \pi r} b dr$$

$$E=\frac{\mu b^2}{4\pi} \ln \left( \frac{R}{r_0} \right)$$

Pour éviter toutes divergences, on introduit un rayon critique en dessous duquel les lois de l’élasticité cessent, on parle du cœur de la dislocation ($r_0$ de l'ordre de $b$ ) et un rayon $R$ de l’ordre de la taille caractéristique du système (distance entre deux dislocations par exemple), soit de l’ordre de 10 à 100000 $b$. Par commodité on prend alors : $\ln(R/r_0)=4\pi$, ce qui conduit à une énergie par unité de longueur :

$$E=\mu b^2$$

Ainsi, allonger une dislocation d’une longueur $dl$, conduit à l’augmentation de son énergie de la quantité $\mu b^2 dl$. Tout se passe comme si une force de rappel (appelée tension de ligne $T= \mu b^2/dl$) s’exerçait sur la dislocation. Les dislocations sont donc de préférence rectilignes. Toutefois, comme il s’agit d’une discontinuité élastique, une ligne de dislocation ne peut s’interrompre dans un cristal : elle forme ainsi une boucle. De la même façon une dislocation $\vec{b}_1$ a tendance à se « séparer » en deux dislocations de vecteurs $\vec{b}_2$ et $\vec{b}_3$ , si on satisfait le critère énergétique :

$$\| \vec{b}_3 \|^2 \ge \| \vec{b}_1 \|^2+\| \vec{b}_2 \|^2$$

Plongée dans un champ de contrainte, un segment de dislocation rectiligne va avoir tendance à se courber selon un arc de rayon $R$. En effet, soumise à ses deux extrémités à une tension de rappel dont la résultante $f$ est dirigée vers le centre du cercle, la dislocation pour rester en équilibre devra être soumise à une contrainte égale et opposée à cette résultante.

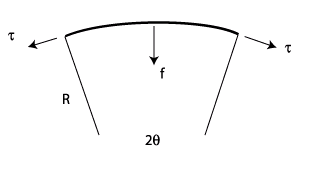
Figure 10

Pour être en équilibre, la dislocation doit donc être soumise à une force par unité de longueur :

$$f=2 T \sin{\theta} \approx 2 \tau \theta= \tau \frac{l}{R}$$

De la même façon, pour étendre une boucle de dislocation de rayon de courbure $R$, la contrainte appliquée doit être supérieure à une certaine contrainte critique. Passées ce cap, elles peuvent alors croître librement. Pensez de la même façon au ballon élastique qui est difficile à gonfler au début, mais s’étend facilement au-delà d’une pression critique. Dans les années 1950, Franck et Read envisagèrent un des premiers modèles de multiplication des dislocations basé sur ce principe. Imaginons pour cela une dislocation ancrée sur deux obstacles rigides et qui se courbe sous l’effet de la contrainte.

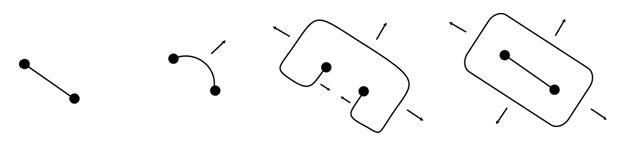
Figure 11

À partir d’une certaine contrainte, l’arc de dislocation s’étend librement aussi bien vers l’avant que sur les côtés et l’arrière, et il arrive un moment où les deux portions arrières se rejoignent et coalescent, donnant naissance à une boucle et un segment de dislocation qui reprend sa forme initiale. Ce « moulin » à dislocations crée donc une série de boucles concentriques.

Durcir un matériau

Les propriétés mécaniques des matériaux s’expliquent grandement à partir des mécanismes élémentaires de dislocations. On comprend par exemple qu’un matériau mou sera caractérisé par de nombreuses dislocations très mobiles (cuivre, aluminium, plomb, or…), un matériau dur par des dislocations peu mobiles (les alliages titane aluminium par exemple) et un matériau fragile par des dislocations trop peu nombreuses et complètement immobiles (les céramiques par exemple). Les matériaux amorphes, comme le verre, qui ne possèdent pas de structure atomique organisée et donc pas de dislocations, sont représentatifs par excellence des matériaux fragiles. La déformation ne peut s’y produire que brutalement par la propagation rapide de fissures. Les mécanismes de durcissement dans les matériaux cristallins sont variés et résultent donc d’une diminution de la mobilité des dislocations. Durcir un métal le rend donc potentiellement plus fragile. Il s’agit alors de trouver un compromis entre une plus grande résistance et une capacité à se déformer. Dans certaines applications (blindage, carrosserie automobile), il est nécessaire d’élaborer des pièces relativement rigides qui gardent la possibilité de se déformer rapidement lors d’un choc. Une des causes du durcissement peut être attribuée aux interactions entre les dislocations. En effet, lorsque la déformation commence, les nombreuses dislocations créées vont interagir pour former un enchevêtrement. Les dislocations finissent par s’immobiliser et le mouvement de nouvelles dislocations est considérablement freiné à la traversée de cette « forêt » de dislocations immobiles. Conclusion, plus la densité de dislocations augmente, plus le mouvement des dislocations est difficile : c’est le phénomène d’écrouissage dont nous parlions en introduction. Il existe bien d’autres paramètres qui influencent le comportement des dislocations, ce qui en fait un sujet d’étude particulièrement complexe et ouvert, au cœur de l’étude des propriétés mécaniques de métaux et alliages.

A lire

Très bonnes introductions (niveau enseignement supérieur) :

• Douin J. Mécanique des milieux continus : introduction à la plasticité des matériaux. Diderot Éditeur.

• Martin J.-L. Dislocations et plasticité des cristaux. Presse Polytechniques Romandes. Un classique des dislocations et de la plasticité :

• Friedel J . Les dislocations. Gauthier-Villars ed.

• De belles simulations numériques de mouvements de dislocations: Micromegas et Numodis

Haut