Le nombre d'or, l'art et la science¶

Cet article est issu de la présentation pour la Fête de la Science au CEMES, 2002.

Introduction: qu'est-ce que le nombre d'or ?¶

Quel est le point commun entre une fleur de tournesol, un tableau de Léonard de Vinci et un quasi-cristal ? Le nombre d'or bien sûr. Un petit voyage dans le monde des nombres, de la géométrie et de la cristallographie nous aidera à y voir plus clair. Mais tout d'abord, je vous propose le petit jeu suivant:

Quel rectangle vous parait le plus harmonieux ? A, B, C .... Le C bien sûr. Voyons un peu en quoi ce rectangle est particulier

Et bien, ce rectangle a des dimensions telles que le rapport de sa hauteur sur sa largeur vaut le "nombre d'or", noté $\phi$ , en l'honneur de l'architecte grec Phidias. Ce nombre vaut approximativement 1.6180339..., c'est un nombre irrationnel, c'est à dire ne s'écrivant pas sous la forme d'une fraction (comme $\pi$ ). Au cours des siècles et surtout au moment de la renaissance, on lui a donné le nom de "divine proportion" (Luca Pacioli)

Le nombre d'or chez les grecs¶

Ce sont les grecs qui ont découvert les propriétés étranges de ce nombre. On l'a bien sûr aussitôt utilisé dans l'architecture pour ses qualités harmonieuses. Par exemple, Phidias, a construit le Parthénon d'Athènes (447 av. j.c.) dans les proportions du nombre d'or. Ici le rapport, entre la largeur de l'édifice et sa hauteur vaut le nombre d'or.

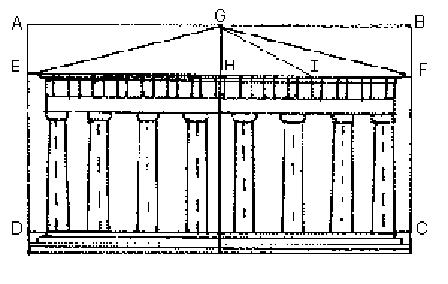
C'est surtout grâce aux travaux du mathématicien grec Euclide, aux alentours de 285 av. j.c. que l'on a découvert le nombre d'or au détour du problème de géométrie suivant: Sur un segment AC, comment placer B, de sorte que le rapport entre le tout et le grand côté soit le même que le rapport entre le grand et le petit côté ? Et bien le point B partage le segment selon la proportion du nombre d'or ! On dit même que le point B forme la section dorée.

Euclide de Megare par Justus Van Gent, 1474

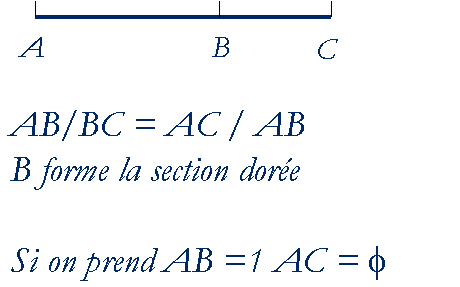
Cette section dorée se retrouve dans beaucoup de situations, mais il est remarquable de voir que l'on peut la remarquer dans le partage du bras ! L'homme serait-il construit selon de divines proportions ? Essayez. On retrouve approximativement le même rapport entre la taille et la hauteur du nombril.

Le nombre d'or et la géométrie¶

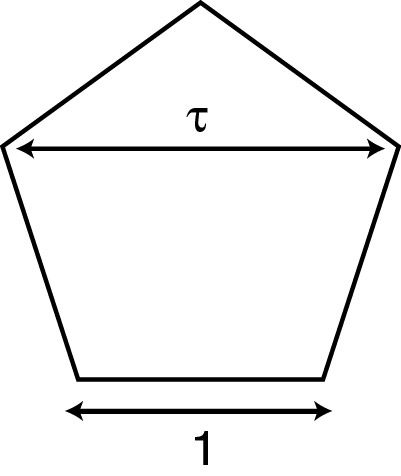
On sait que les grecs furent de grands géomètres et certains d'entre eux, les pythagoriciens, furent tellement séduits par la beauté des nombres en particulier celle du nombre d'or, qu'ils décidèrent de faire du pentagone leur emblème. Et oui, dans le pentagone on retrouve le nombre d'or. Ainsi la nature exprime elle aussi les propriétés du nombre d'or, admirez ce squelette d'oursin pentagonal.

Voici une propriété intéressante du nombre d'or: Prenez un rectangle d'or ( $L/l = \phi$ ). Enlevez lui le carré de plus petit côté, et bien figurez-vous que le rectangle restant est un rectangle d'or ! On peut ainsi continuer l'opération à l'infini. Et si maintenant on souhaite relier les côtés opposés des carrés on obtient une spirale logarithmique, dite spirale d'or. Saviez-vous que la corne de bouquetin et la coquille du nautile reproduisaient cette spirale ?

Le nombre d'or et la reproduction des lapins¶

Le nombre d'or a évidemment intéressé les mathématiciens, mais parmi eux, Leonardo Fibonacci (1170-1250) s'est illustré dans l'analyse du problème de la reproduction des lapins. Voici comment il en parle: « Possédant au départ un couple de lapins, combien de couples de lapins obtient-on en douze mois si chaque couple engendre tous les mois un nouveau couple à compter du second mois de son existence ? »

Prenons un couple de lapins, au bout d'un mois, les lapins peuvent se reproduire, et donnent un nouveau couple qui peut se reproduire de nouveau au bout d'un mois etc....

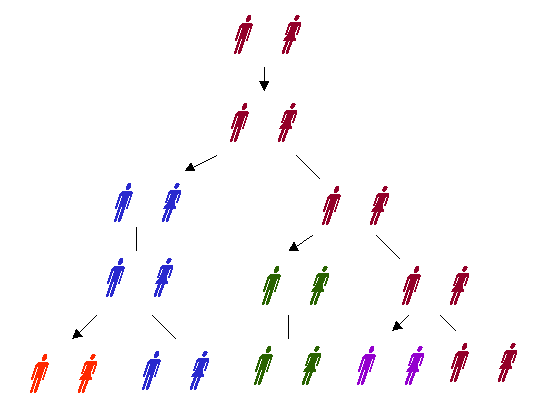
Le nombre de couple de lapins évolue selon une suite, dite suite de Fibonacci: 1, 1, 2, 3, 5......Amusez vous maintenant à calculer le rapport des termes successifs: 1/1=1, 2/1=2, 3/2=1.5, 5/3=1.666..., 8/5=1.6 etc..., il est clair que ce rapport tend vers le nombre d'or ! Voilà un bel exemple où l'évolution de populations a un rapport avec ce nombre. Même si le problème ne semble pas très réaliste (les lapins seraient-ils consanguins et immortels ?), il peut s'appliquer de façon plus approchée chez les abeilles.

Le nombre d'or dans la nature¶

Avez-vous fait attention à la fleur de tournesol ? Elle s'arrange en spirales. Des spirales qui partent du centre et qui vont vers l'extérieur en tournant vers la gauche et d'autres qui tournent vers la droite. Comptez maintenant le nombre de spirales dans les deux sens. Miracle ! Le rapport 34/21 vaut 1.619 ce qui est très proche du nombre d'or ! (en fait vous avez reconnu 2 termes successifs de la suite de Fibonacci). Essayez, ça marche avec les pommes de pin aussi.

Le nombre d'or en peinture¶

Les peintres de la renaissance surtout en Italie ont cédé à l'appel quasi mystique du nombre d'or pour construire leurs tableaux. Par exemple dans l'Annonciation de Léonard de Vinci (galerie des Offices, Florence), si l'on découpe les côtés du tableau selon les proportions du nombre d'or, on obtient des lignes qui délimitent l'emplacement des personnages (lignes verticales) ou qui définissent la ligne des épaules, des mains ou des genoux (lignes horizontales).

© Galerie des Offices, Florence

Le monde des cristaux¶

© Geowiki

Je suis sûr que vous avez déjà vu des cristaux. Ici c'est un cristal de quartz. Remarquez l'élégance des facettes qui le composent. Son étonnante beauté n'est en rien troublée par l'ordre militaire qui y est instauré jusqu'à son échelle la plus fine, celle de ses atomes.

Prenez le sel, qui est lui aussi un cristal. Faites un zoom jusqu'à l'échelle atomique. Qu'obtient-on ? Et bien un arrangement des atomes selon un motif clairement défini sur un réseau.

Ici le réseau est composé de "mailles" de forme cubique avec des atomes verts (chlore) sur les sommets et aux centres des faces et des atomes gris (sodium) sur les arêtes et au milieu du cube. Cette construction est tout à fait analogue à celle que l'on fait lorsqu'on construit un carrelage (ou pavage) ou une tapisserie ! Elle peut être résumé par la formule: Pavage = un motif + une maille. Dans la suite on prendra toujours l'exemple à 2 dimensions.

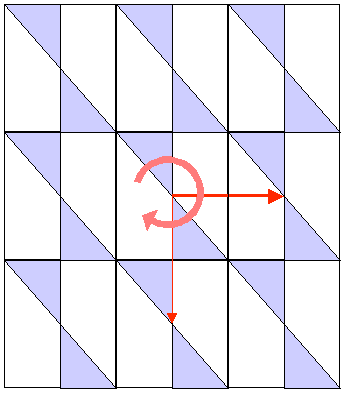
Comment construire un pavage du plan ? C'est simple, on prend une maille, ici rectangulaire, dans laquelle on dessine un motif, ici un papillon violet. Ceci fait apparaître la 1ère propriété du pavage. Une symétrie de rotation (ici 180° par rapport au centre). On parle aussi de symétrie d'orientation. Ensuite on déplace le pavé élémentaire dans 2 directions du plan définies par les 2 côtés de la maille. Ceci fait apparaître la deuxième propriété du pavage. C'est la symétrie de translation. On obtient ainsi un pavage du plan périodique, c'est à dire qui se répète dans les deux directions.

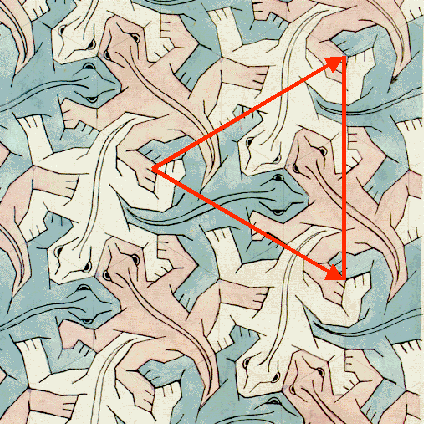
Pour se convaincre de la notion de symétrie dans les pavages, regardons deux beaux pavages que le dessinateur M.C Escher nous a laissés.

© M.C Escher

Dans le pavage de droite, on voit clairement une alternance d'hommes debout. Si l'on fait abstraction des couleurs, on remarque clairement, la symétrie de rotation de 180° (par exemple autour du coude) et les symétries de translation (entre les hommes rouges et blancs verticalement par exemple). Sur le pavage de gauche, la symétrie de rotation est de 120° autour des têtes de lézard par exemple et les deux translations forment une maille triangulaire.

On vient de voir l'importance des notions de symétrie pour classer les pavage. Sachez que ces seules notions permettent de construire l'ensemble des pavages périodiques réguliers. On dit que l'ensemble de ces pavages sont représentés en mosaïque à l'Alhambra de Grenade. Dans l'espace à 3 dimensions, on peut classer de façon exhaustive l'ensemble des structures cristallines avec les mêmes critères. Ce lourd travail a été en partie effectué par le cristallographe français à la fin du 19ème siècle: Auguste Bravais. On trouve ainsi 230 types de cristaux différents ! (pour plus de détails sur l'histoire de la cristallographie, rendez vous dans la section suivante). Revenons à notre pavage du plan. Peut-on construire n'importe quel pavage régulier et périodique avec n'importe quel type de pavé ?

Comme on peut le voir ici, il est clair que l'on peut construire un tel pavage avec des rectangles, des triangles, des carrés et des hexagones (structure en nid d'abeille). Mais qu'en est il des pavages de pentagones ?

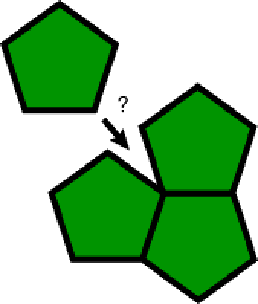
Cela est impossible ! Car si l'on tente d'accoler des pentagones et bien on voit que les pavés vont se recouvrir ou laisser des vides. N'a t'on pas dit que le nombre d'or se retrouvait dans le pentagone? Notre espoir de retrouver le nombre d'or dans les cristaux vient donc de s'envoler. En réalité pas tout à fait. Les choses sont un peu plus compliquées et le nombre d'or peut se retrouver non pas dans les cristaux mais dans les quasi-cristaux.

Les quasi-cristaux¶

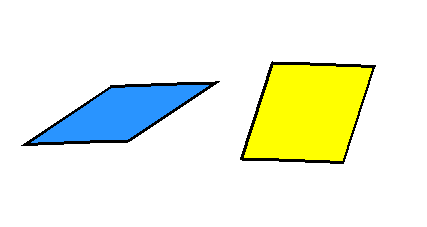
La prouesse a été réalisée en 1974, par un mathématicien anglais Sir Roger Penrose. Il a réussi à construire un pavage avec deux types de briques (les losanges bleus et jaunes) de telle sorte que l'ensemble soit non-périodique (pas de symétrie de translation) mais qui exhibe la symétrie de rotation du pentagone ! Formidable, non ?

Dans un pavage de taille infini, le rapport entre le nombre de pavés jaunes sur le nombre de pavés bleus est, ....... le nombre d'or ! Ceci est une construction totalement mathématique, mais comme nous allons le voir, ce type d'arrangement existe bel et bien et on les appelle les quasi-cristaux.

© World of Escher

© Ames Lab

En 1982, en travaillant sur des échantillons trempés à base d'aluminium, Dan Shechtman (prix Nobel de Chimie 2011), un chercheur israélien, découvre la symétrie pentagonale jusque là interdite ! Les quasi-cristaux sont nés... On en trouve de très grandes variétés. Ils exhibent des facettes de croissance, comme pour les cristaux, mais de forme pentagonale ! Voilà, notre périple se termine, nous avons finalement retrouvé le nombre d'or dans l'organisation même de la matière dans les quasi-cristaux, allez savoir pourquoi ce nombre se glisse partout, en tout cas depuis les grecs un bout de chemin a été parcouru et ce nombre nous fascine toujours.