L'hypothèse du glissement¶
Schmid et Boas¶
Lorsque les physiciens du début du siècle regardaient des éprouvettes déformées en traction, les images de leurs surfaces prises en microscopie (optique) révélaient de fines stries.

Des traces de glissement dans un cristal de Cadmium (DoITPoMS.ac.uk)
Ceci est tout à fait compréhensible dans l’hypothèse de la rame de papier comme nous l’avons vu. En effet, dans ce type d’expérience, on s’attend intuitivement à un comportement illustré sur la figure suivante : on forme des marches à la surface.

La question qui a alors intriguée les métallurgistes était de savoir pourquoi les lignes de glissement apparaissaient dans des directions particulières par rapport à l’axe de traction. On constate dans les matériaux cubiques à faces centrées en traction selon une direction de type (100) que le glissement s’amorce toujours dans les plans de type (111) et dans une direction de type [110] (c'est-à-dire à 45°). Le glissement se propage dans les plans denses et dans une direction où les atomes sont les plus proches.
En étudiant un grand nombre de situations, Schmid et Boas ont établi une loi générale qui nous dit: que le glissement apparaît toujours dans le plan pour lequel la contrainte est maximum. Par exemple les systèmes [110](111) sont ceux qui sont activés en premier lorsque la contrainte appliquée est selon (100).
Un peu plus loin¶
Comme le glissement s’effectue dans des plans particuliers, c’est la contrainte résolue dans ce plan qui est importante. Elle s’écrit simplement :
où m est appelé le facteur de Schmid, \psi l’angle entre la direction de la contrainte appliquée et la normale au plan de glissement et l l’angle entre la direction de la contrainte appliquée et la contrainte résolue. En glissement, la contrainte résolue est maximum et égale à la moitié de la contrainte appliquée lorsque \psi=\lambda=45^\circ.
L’énigme du glissement¶
Il est clair que la déformation plastique nécessite un réarrangement important de la matière. Pourtant, cette situation semble paradoxale dans les métaux, où la structure interne (celle d’un cristal où les atomes sont répartis sur un réseau périodique tridimensionnel) doit être conservée malgré les changements de forme extérieure. La façon la plus intuitive d’imaginer la déformation est de considérer qu’elle procède par une série de glissements élémentaires le long de plans atomiques, à la manière des feuilles d’une rame de papier qui glissent les unes sur les autres.
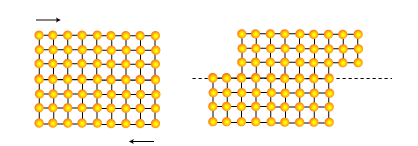
Partons du cas le plus simple d’un cristal cubique simple, et déplaçons en cisaillement la partie supérieure de la quantité ''x'' par rapport à la partie inférieure. Pour effectuer un tel déplacement, il est nécessaire d’amener les atomes de la partie supérieure en contact avec ceux de la partie inférieure dans une position instable (position de col). Chaque atome du plan cisaillé doit donc "grimper" une barrière d'énergie comme schématiquement illustré ci dessous.
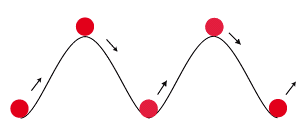
En terme mathématique, on exprime la contrainte nécessaire pour déplacer un atome dans ce potentiel par une fonction périodique et qui est minimale chaque fois que l’on s’est déplacé d’une distance interatomique dans le sens du mouvement :
\mu (le module de cisaillement) étant une constante mesurant l’aptitude d’un matériau au cisaillement. Il est typiquement de l’ordre de la centaine de tonnes par cm^2 . En supposant pour les petits déplacements que la déformation est élastique, on peut écrire :
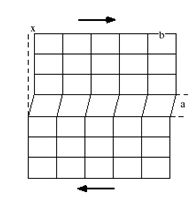
On obtient finalement :
La valeur maximum de cette contrainte est alors \tau=0.2 \mu soit mille à dix mille fois plus que la valeur expérimentale ! Si la déformation était purement élastique, on pourrait suspendre une automobile à un fil cylindrique d’aluminium de 1 mm de rayon !