Durcir un métal

Il y a en fait deux types de forces qui peuvent s’opposer au mouvement des dislocations. La première est la friction du réseau et la seconde est la force nécessaire au franchissement d’obstacles.

La friction du réseau résulte simplement du fait qu’il faille fournir un peu d’énergie aux dislocations pour cisailler le cristal, c'est-à-dire couper et recoller des liaisons atomiques. Dans les métaux, la friction du réseau est faible car les liaisons ne sont pas « trop » directionnelles et « trop » difficiles à rompre. En conséquence, ce sont des matériaux plutôt mous (cuivre, aluminium, plomb…). L’origine du durcissement est ailleurs. Nous reparlerons plus tard des forces de friction.

Le plus simple est de considérer les dislocations elles-mêmes comme leur propre obstacle à leur propagation. Les interactions entre les dislocations conduisent à la création comme nous l’avons d’obstacles importants : ancrage, points d’épinglage, formation de dipôles, débris de dislocations, mécanisme de la forêt…. Nous avons regroupé l’ensemble de ces phénomènes sous le terme de durcissement par écrouissage.

Simulation du franchissement de la forêt, P. Guyot, Yravals 1979

De la même façon, la formation de boucles sessiles par dégâts d’irradiation entraîne un durcissement. Ceci peut conduire de façon catastrophique à une fragilisation et à des problèmes de fissuration des cuves de réacteur.

Imaginons quelle contrainte est nécessaire pour franchir une forêt de dislocations. On peut raisonnablement considérer qu’une dislocation sur deux de la forêt va conduire à un ancrage fort (type jonction attractive) entre lesquels une dislocation mobile va se courber. La distance moyenne entre les dislocations va être de l’ordre de $2L$ ($L$ étant la distance entre les dislocations). Pour que les dislocations se « désancrent », il faut alors que son rayon de courbure $R$ soit de l’ordre de $L$.

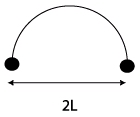
La distance entre les dislocations peut être exprimée en fonction de la concentration de dislocations par unité de longueur $\rho$ (en supposant qu’elles sont équiréparties dans le cristal) par:

$$L=\frac{1}{\sqrt{ \rho}}$$

La contrainte à fournir est donc :

$$\tau= \frac{T}{Lb}=\alpha \mu b \sqrt{\rho}$$

où $\alpha$ est un coefficient valant de l’ordre de 0.2 à 0.3. Cette loi, appelée loi de Taylor, est en fait plus générale et s’applique à tout type de durcissement en considérant des valeurs de $\alpha$ variant dans une gamme plus large en fonction du mécanisme.

On peut concevoir également la création de verrous. Dans les métaux cubiques à faces centrées, les verrous de Lomer-Cotrell sont particulièrement rencontrés. Ils se forment lorsque deux dislocations $1/2 [110]$ dissociées dans des plans $(111)$ se rencontrent. Elles créent alors une dislocation de type $1/6 [011]$ sessiles. Dans la représentation de Thomson, leurs vecteurs de Burgers sont représentés par les vecteurs joignant les faces du tétraèdre.

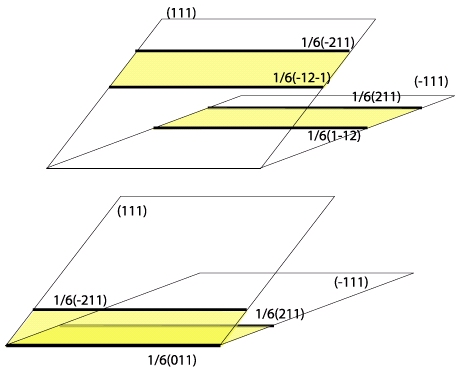
Le phénomène d’écrouissage est responsable du durcissement d’un bon nombre de métaux purs. Il est responsable par exemple du durcissement du fer dit forgé. A haute température, le martelage de la phase stable du fer qui est cubique à faces centrées (fer gamma) entraîne la formation de nombreuses dislocations $1/2[110]$. En trempant l’échantillon, on transforme la phase $\gamma$ en phase a qui est cubique centrée. Les dislocations ainsi piégées deviennent sessiles dans cette phase.

Le durcissement d’un cristal peut être du également par la présence d’obstacles extrinsèques : il s’agit de précipités ou d’atomes étrangers.

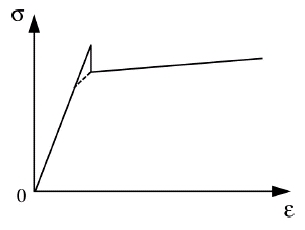
Les atomes d’impureté (pour les mêmes raisons que les lacunes) viennent trouver une position plus stable au niveau des dislocations. Par exemple un gros atome trouvera une position plus stable au niveau de la zone en tension engendrée par une dislocation coin. Lorsque la dislocation rencontre ces atomes, il devient alors plus difficile de la déplacer. Ainsi en début de déformation, il est nécessaire de fournir une contrainte plus grande que dans un matériau pur pour initier la déformation. La courbe de traction de ce type de matériau présente donc un crochet de traction.

Nous reviendrons sur l’influence de la température sur ce mécanisme. On connaît bien un grand nombre d’applications utilisant l’ajout d’impuretés pour durcir un métal. Par exemple l’or qui est un métal extrêmement mou, devient rigide lorsqu’il contient du cuivre, du nickel ou du platine. En général la contrainte critique augmente avec la concentration $c$ d’impuretés selon $c \times m$ ($m$ de l’ordre de 0.5 à 0.7).

Pour l’instant, nous n’avons parlé de durcissement par une solution solide où les atomes d’impureté occupent une position quelconque dans la matrice, en d’autres termes, si le matériau est désordonné. Toutefois, un durcissement supplémentaire apparaît si ces atomes préfèrent occuper des sites particuliers que ce soit à courte ou à longue distance. Rappelez-vous maintenant ce que nous avons dit sur les alliages ordonnés. Imaginons un précipité binaire A-B ordonné dans une matrice A. Supposons maintenant qu’une dislocation de vecteur de Burgers AA=AB vienne cisailler ce précipité. Elle crée un défaut d’empilement qui est un peu particulier que l’on appelle une paroi d’antiphase. La création de cette faute nécessite une énergie correspondant à la mise en désordre chimique du précipité. Ceci entraîne bien entendu un durcissement. Toutefois, on comprend aisément que le passage d’une seconde dislocation va restaurer cet ordre, en conséquence de quoi le durcissement est modéré.

Le passage de l’alliage désordonné à l’alliage ordonné s’effectue à une température bien précise. Lorsque cette température est localement atteinte dans une partie du cristal, des domaines d’ordre se propagent. Les parois d’anti-phases apparaissent alors naturellement lorsque différents domaines se rencontrent.

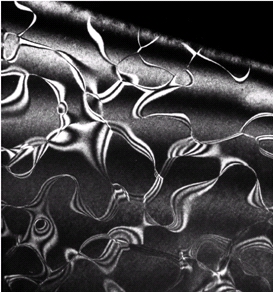
Parois d’antiphases dans $Cu_3Pd$, A. Loiseau, ONERA

On comprendra alors aisément d’après le schéma suivant que le franchissement d’une paroi d’antiphase par une dislocation contribue à un durcissement par mise en désordre.

Si maintenant la concentration en impuretés augmente encore, les atomes ont tendance à s’agréger pour minimiser l’énergie du système. On forme alors des précipités. Lorsqu’ils ont une structure incompatible avec le reste du cristal (précipités incohérents), ils sont particulièrement efficaces pour empêcher le mouvement des dislocations, à cause de leur champ élastique. Nous avons vu que les dislocations pouvaient les cisailler (pour les plus petits) ou les contourner (pour les plus gros et les plus durs). Le cisaillement des précipités n’entraîne pas un durcissement très important car une fois les précipités cisaillés, les dislocations suivantes vont pouvoir passer aisément. Au contraire le contournement d’un précipité conduit à la formation d’une boucle résiduelle autour du précipité (appelée boucle d’Orowan) qui est un obstacle supplémentaire pour les dislocations suivantes.

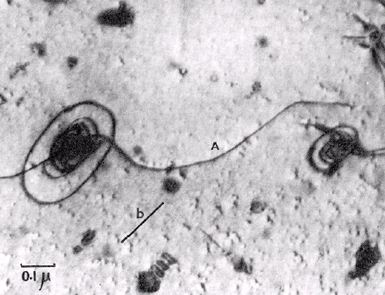
Boucles d’Orowan autour de précipités

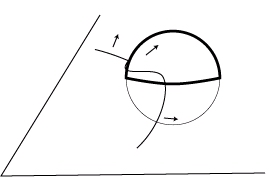
Le franchissement d’un précipité peut nécessiter également les mécanismes de glissement dévié ou de montée. Nous en reparlerons à propos des mécanismes thermiquement activés.

Il y a de nombreuses applications de durcissement par précipitation : les alliages d’aluminium (les Duralumins) pour l’aéronautique, les superalliages (précipités cubiques centrés ordonnés dans une matrice cubique centrée désordonnée), les matériaux composites métal céramique…