Quand les dislocations interagissent

Les dislocations isolées, étant des singularités élastiques dans le cristal, développent autour d’elle un champ élastique à longue distance de portée infinie, comme un électron est entouré d’un champ électromagnétique. Une dislocation vis, par exemple développe des contraintes élastiques de la forme :

$$\sigma \propto \frac{\mu b}{2\pi r}$$

On voit que la contrainte est proportionnelle au vecteur de Burgers (ce qui est analogue à la charge électrique), au module de cisaillement qui nous dit si le cisaillement est facile ou pas (analogue à la permittivité électrique du milieu), et inversement proportionnelle à la distance. Le facteur $2\pi$ provient de la symétrie cylindrique du champ élastique autour de la dislocation.

Comme les dislocations possèdent un champ élastique, elles interagissent avec un champ extérieur ou avec le champ d’autres dislocations. Voyons un peu comment. On procède selon l’approche newtonienne des forces qui consiste à regarder quel est le travail d’une dislocation lorsqu’on la déplace (plus simplement, on regarde quelle quantité d’énergie il faut pour déplacer une dislocation sur une distance $l$)

Intéressons nous d’abord à l’interaction d’une dislocation avec un champ de contrainte extérieur. Raisonnons en premier lieu de manière simplifiée et considérons une dislocation traversant complètement un échantillon de dimension $L$ sur $l$ sous l’influence d’une contrainte extérieure de cisaillement $\tau$.

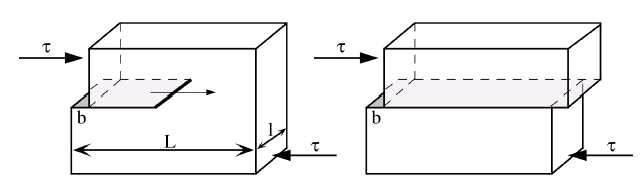
© Mécanique des milieux continus, J. Douin

En traversant l’échantillon, les deux parties de l’échantillon ont été déplacées d’une quantité b. Le travail $W_a$ de la force appliquée $F_a$ sur l’échantillon est donc :

$$W_a=F_a b =\tau S b=\tau (Ll) b$$

Ce travail est égal à celui de la force $F$ nécessaire pour déplacer la dislocation de longueur $l$ sur la distance $L$, et qui s’écrit :

$$W=FL$$

Ceci nous conduit alors à l’expression de la force (par unité de longueur) exercée sur une dislocation par une contrainte extérieure :

$$\frac{F}{l}=\tau b$$

Dans le cas général, cette formule doit être remplacée par la formule de Peach et Koehler pour tenir compte de l’orientation de la contrainte par rapport à la dislocation et son vecteur de Burgers:

$$\left( \vec{b} \cdot \overline{\overline{\sigma}} \right) \times \vec{u}$$

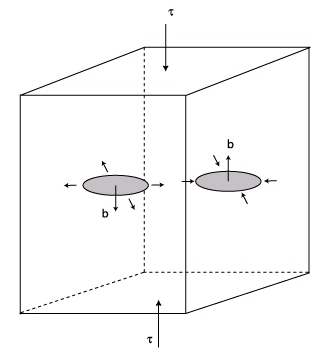
Pour illustrer cette formule, considérons une boucle de dislocation de vecteur de Burgers, perpendiculaire au plan de la boucle, et une contrainte uniaxiale parallèle à $\pm \vec{b}$ selon l’axe $z$. La force subie par la boucle est alors :

$$F= \pm \mu b \left( \begin{matrix} 0&0&0\\ 0&0&0 \\ 0&0&1 \end{matrix} \right) \left(\begin{matrix} 0 \\ 0 \\1 \end{matrix}\right) \times \left(\begin{matrix} u_x \\ u_y \\0 \end{matrix}\right)$$

$$F= \pm \mu b \left( \begin{matrix} -u_y \\ u_x \\0 \end{matrix}\right)$$

La force qui s’exerce sur la boucle est radiale et se trouve dans son plan. Elle tend à la faire croître si $\vec{b}$ est orienté dans le même sens que la contrainte et à la faire se contracter dans le cas contraire. Vous remarquerez au passage qu’il s’agit d’un processus de montée.

Que se passe- t’il maintenant lorsque deux dislocations interagissent ? Il suffit d’exprimer la formule de Peach et Koehler en écrivant la force agissant sur la seconde dislocation lorsqu’elle est plongée dans le champ de contrainte de la première. Prenons comme exemple deux dislocations vis parallèles séparées d’une distance $R$. Le champ de contrainte de la seconde dislocation est de la forme $\sigma$ prop. $\mu b^2/R$ de sorte que la force d’interaction est après calcul :

$$\vec{F}= \frac{\mu \vec{b}_1 \vec{b}_2}{2 \pi R^2} \vec{R}$$

Cette force est radiale et décroissante en $1/R$ (elle ne dépend que de la distance entre les dislocations). Elle est attractive si les vecteurs de Burgers sont opposés et répulsive dans le cas contraire. Ceci nous explique pourquoi nos deux dislocations s’annihilent dans la séquence vidéo. Dans le cas de deux dislocations coins, la situation est légèrement plus compliquée, mais on peut en tirer des conclusions intéressantes. Le schéma suivant résume les différents cas de figure.

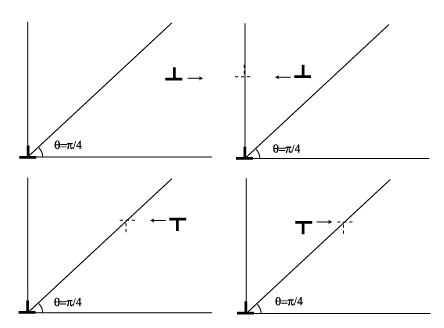
Lorsque les deux dislocations ont des vecteurs de Burgers de même signe, elles se stabilisent l’une au dessus de l’autre. Une situation intéressante apparaît lorsqu’un grand nombre de dislocations s’empilent de cette façon les unes sur les autres. Elles conduisent à la configuration suivante (volontairement exagérée):

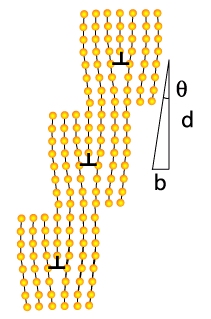
Cet empilement conduit donc à une désorientation (faible) de la partie droite de la figure par rapport à la partie gauche d’un angle $\theta=b /d$, où $d$ est la distance entre les dislocations. On appelle ce genre de configuration un sous joint de flexion. Il existe d’autre type de sous joint si l’on considère des situations plus complexes impliquant des réseaux de dislocations coins et vis. Ils engendrent alors des rotations plus complexes entre les deux parties du cristal.

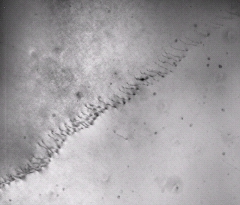
Cliché CEMES

Lorsque les dislocations ont des vecteurs de Burgers de signe opposé, on remarque qu’elle trouve une position d’équilibre à 45°. Elles forment alors ce que l’on appelle un dipôle de dislocations. La formation de dipôle est particulièrement intéressante car on remarque que pour briser un tel dipôle il est nécessaire de fournir une contrainte supérieure à $\sigma= \mu \vec{b}_1 \vec{b}_2/2\pi (1-\nu)R$. On verra que ceci a son importance en plasticité.

Un autre type d’empilement est intéressant à regarder car il se rencontre fréquemment. Prenons plusieurs dislocations glissant dans le même plan avec le même vecteur (elles proviennent d’une même source comme nous le verrons) sous l’effet d’une contrainte externe. Supposons maintenant que la dislocation de tête s’arrête pour sur un obstacle (nous parlerons des obstacles plus tard). Les dislocations suivantes vont venir s’empiler les unes derrière les autres à cause de leurs interactions répulsives. La configuration qu’elle forme est grossièrement la suivante :

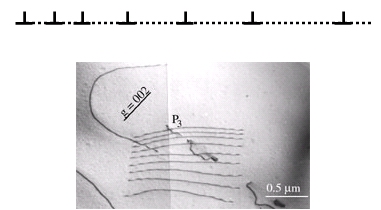
Cliché CEMES

On constate que les dislocations ne sont pas réparties de façon équivalente. La taille d’un empilement est en fait proportionnelle au nombre de dislocations et inversement proportionnelle à la contrainte appliquée. Autre point important : la dislocation de tête concentre les contraintes et tout se passe comme si elle était soumise à $n$ fois la contrainte d’une dislocation. Nous reviendrons sur ces empilements.

Nous n’avons pour l’instant rien dit lorsque deux dislocations se rencontraient, soit parce qu’elles s’attirent, soit parce qu’elles sont soumises à une contrainte qui les oblige à se rencontrer.

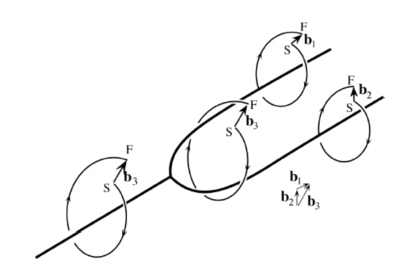
© Mécanique des milieux continus, J. Douin

Lorsque deux dislocations se rencontrent, soit elles « s’accouplent » pour donner naissance à une troisième dislocation, et l’on parle alors de jonction attractive, soit elles ne s’aiment guère et font tout pour s’éviter : c’est une jonction répulsive.

Le vecteur de Burgers doit (toujours) être conservé lors d’une réaction de jonction. Il s’ensuit qu’à un nœud entre plusieurs dislocations, la somme des vecteurs de Burgers est nulle (ceci est analogue à la loi de Kirchhoff en électricité).

Pour donner un exemple de réaction de jonction attractive, prenons deux dislocations $\vec{b}_1$ et $\vec{b}_2$ attractives qui forment un croisement. Elles donnent un segment de dislocation de vecteur $\vec{b}_1 - \vec{b}_2$.

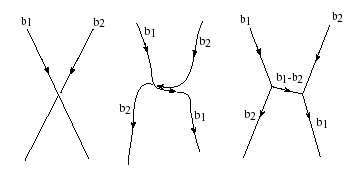
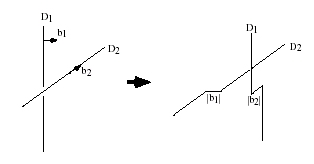
Pour poursuivre le mouvement, on doit effectuer le processus inverse (il faut en quelque sorte « dézipper » la jonction), ce qui nécessite une contrainte supplémentaire. Cette réaction constitue donc un obstacle fort à la poursuite du mouvement. Dans le cas d’une jonction répulsive, aucun nouveau segment n’est formé, mais chaque dislocation imprime à l’autre un cran égal à son vecteur de Burgers. La jonction répulsive constitue elle aussi un obstacle au mouvement.

Dans les deux cas que nous venons de rencontrer, la nouvelle portion de dislocation apparaissant peuvent être temporaires ou non. En réalité, tout cela dépend si ces segments sont glissiles ou sessiles. Il se forme alors des ancrages ou des points d’épinglage qui peuvent être éliminés par des mécanismes différents dont nous parlerons plus tard.