Cristallographie élémentaire¶
Le modèle le plus simple de structure atomique d’un cristal consiste à assimiler les atomes comme des sphères dures en contact les unes avec les autres. C’est le problème du tas d’orange. Dans le plan, la façon la plus simple est de former un réseau hexagonal. C’est le réseau le plus compact.
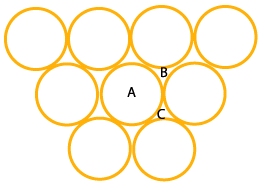
Pour créer un empilement, il faut placer de nouveaux atomes sur la première couche. On a deux possibilités : soit les mettre dans la position B soit dans la position C (ce sont des positions équivalentes). On peut réaliser alors deux types d’empilement: celui de type ABABABA… ou de type ABCABC…
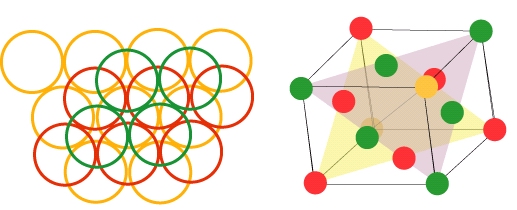
Si on regarde l’empilement ABCABC…obtenu le long de la diagonale d’un cube, on s’aperçoit que les atomes sont répartis sur les sommets et le centre des faces du cube (on représente les atomes un peu distant les uns des autres pour plus de clarté). On dit que l’on a une structure cubique faces centrées. C’est une structure fréquemment rencontrée dans les cristaux. Le cuivre, l’aluminium, le plomb, le fer dit « gamma»… cristallisent selon cette structure.
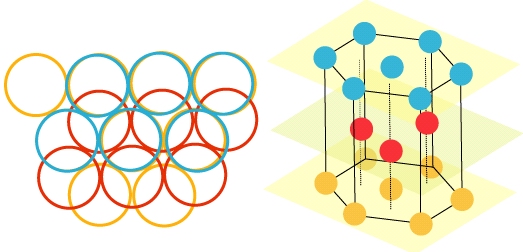
La structure ABAB… est appelée quant à elle structure hexagonale compacte. C’est celle du magnésium, du calcium, du zinc, du titane…
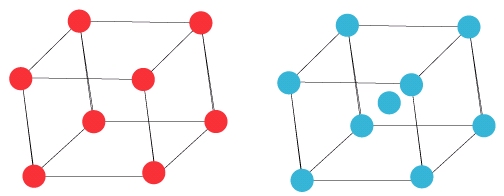
Il existe d’autres structures plus simples comme la structure cubique (les atomes sont sur les sommets du cube) (c’est le cas du manganèse ou de l’uranium) ou la structure cubique centrée (les atomes sont sur les sommets et le centre du cube) (c’est le cas chrome, du tungstène, du fer dit « alpha »).
Bien sûr il existe des composés contenant plusieurs types d’atomes : on parle alors d’alliages s’il s’agit de plusieurs métaux. Lorsque l’alliage est dit « ordonné », les atomes occupent des sites bien déterminés dans les structures décrites précédemment. Par exemple dans l’alliage fer-aluminium (FeAl), les atomes de fer occupent le centre du cube et les atomes d’aluminium les sommets.
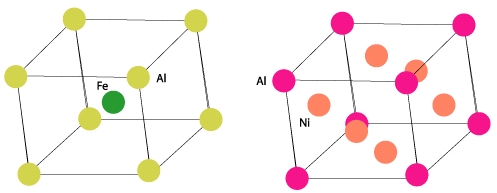
Lorsque l’alliage est désordonné, les atomes d’une espèce occupent indifféremment leurs sites ou ceux des autres espèces. L’alliage FeAl pourrait alors ressembler à la figure suivante par exemple (attention il faut voir ici la structure de l’alliage comme étant l’imbrication de deux structures cubiques simples)
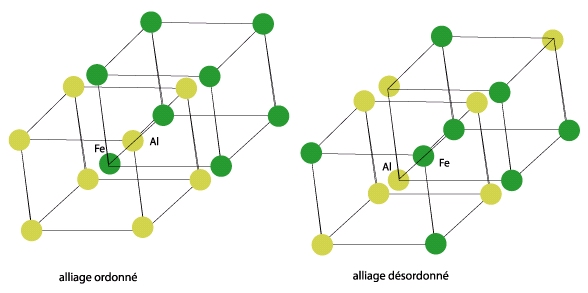
Comme nous le verrons plus tard, déformer un alliage introduit des réarrangements atomiques, qui dans certains cas s’accompagne d’une mise en désordre de la structure. Le rôle de la mise en désordre est un sujet de questionnement indispensable pour bien comprendre la plasticité d’un alliage (nous en reparlerons).
Pour aller plus loin …¶
Nous avons vu que les structures des alliages pouvaient se construire par un empilement approprié de couches atomiques. Ces couches d’atomes sont appelées des « plans atomiques ». On peut définir autant de plans atomiques en fait si l’on considère la surface formée par deux vecteurs dans un repère (Ox, Oy, Oz) en prenant comme origine (et pour faire simple en considérant que les structures cubiques) un sommet du cube élémentaire. Tous les plans ne contiennent pas le même nombre d’atomes, et les plans les plus denses sont ceux qui correspondent aux plans les plus éloignés. On verra par la suite que la déformation est principalement localisée dans ces plans. Pour la structure cubique faces centrées, les plans denses correspondent aux plans perpendiculaires à la diagonale du cube. Le vecteur unité normal à ces plans est dans le repère (Ox, Oy, Oz) :
La constante a est appelée le paramètre de maille du réseau. Ici il s’agit de la longueur du côté du cube élémentaire. Il est généralement de l’ordre du dixième de milliardième de mètre !
On note cette direction entre crochet : [111] et la famille de plans correspondant entre parenthèses (111).
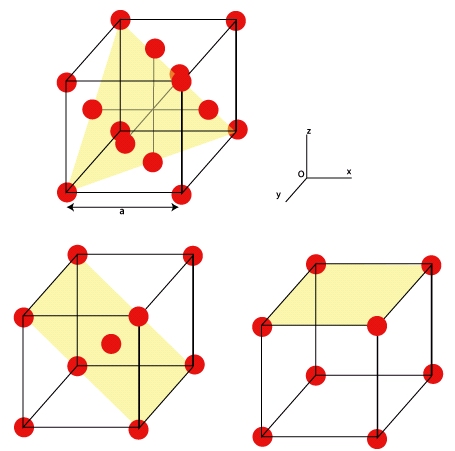
A votre avis quels sont les plans denses dans la structure cubique simple et cubique centrée ? Réponse : (001) et (101).
Bien sûr vous aurez peut être remarqué qu’il y a plusieurs plans denses pour une structure donnée. Si on prend la structure cubique faces centrées, l’ensemble des plans denses forment un polyèdre appelé tétraèdre de Thomson.
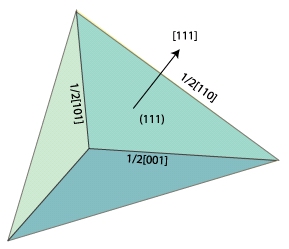
Les arrêtes de ce tétraèdre représentent les vecteurs joignant deux atomes le long de la diagonale d’une face. Il s’agit des plus petites translations dans le réseau cubique faces centrées. On verra dans la suite l’importance de ces translations.