Arc, corde et tension de ligne

Jusque là, nous n’avons pas parlé de l’aspect énergétique des dislocations. Commençons par définir l’énergie élastique stockée dans une dislocation. Pour une dislocation vis, le travail effectué pour déplacer les deux parties du cristal d’une distance b est donné par :

$$E=\frac{1}{2} \int_{r_0}^R \tau b dr = \frac{1}{2} \int_{r_0}^R \frac{\mu b}{2 \pi r} b dr$$

$$E=\frac{\mu b^2}{4\pi} \ln \left( \frac{R}{r_0} \right)$$

Où $R$ est une distance quelconque et $r_0$ est le rayon du cœur de la dislocation. On constate que cette formule diverge ! Dans le cristal réel, plusieurs raisons interviennent pour limiter l’énergie d’une dislocation. On peut penser simplement que les dislocations sont des boucles, et que chaque partie de la boucle forme un dipôle avec la partie opposée. On se doute alors que les champs élastiques vont se compenser partiellement et que l’énergie de la boucle va rester finie. Le fait que l’énergie soit finie tient également au fait que l’échantillon a des bords. En effet, pour que les contraintes soient nulles à la surface, tout se passe comme si on avait introduit par la pensée une dislocation de signe opposée à l’extérieur de l’échantillon. La surface exerce donc sur la dislocation la même interaction qu’exercerait la dislocation « image » placée en position miroir de la première. En conclusion, on peut considérer que toutes les dislocations sont appariées.

Typiquement on choisira donc $R$ comme étant la distance moyenne entre les dislocations, soit $R$ de l’ordre de 10 à 100000$b$ et $r_0=b$. Par commodité on prend alors : $\ln(R/r_0)=4\pi$, ce qui conduit à :

$$E=\mu b^2$$

L’énergie élastique dont nous parlons ici est une énergie par unité de longueur. Ainsi, allonger une dislocation d’une longueur $dl$, conduit à l’augmentation de son énergie de la quantité $\mu b^2 dl$. Ainsi en l’absence de contrainte extérieure, la dislocation tend à être rectiligne pour minimiser son énergie. Tout se passe comme si une force de rappel (appelée tension de ligne $T= \mu b^2/dl$) s’exerçait sur la dislocation. La dislocation se comporte un peu comme une corde. Plongée dans un champ de contrainte, la dislocation va avoir tendance à se courber selon un arc de rayon $R$. En effet, soumise à ses deux extrémités une tension de rappel dont la résultante $f$ est dirigée vers le centre du cercle, la dislocation pour rester en équilibre devra être soumise à une contrainte égale et opposée à cette résultante.

$$f=2 T \sin{\theta} \approx 2 \tau \theta= \tau \frac{l}{R}$$

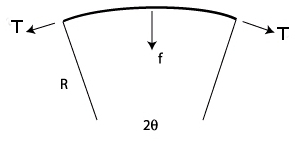
Pour être en équilibre, la dislocation doit donc être soumise à une force par unité de longueur :

$$F=\frac{\mu b^2}{R}$$

La tension de ligne explique alors pourquoi les petites boucles qui ont un petit rayon de courbure doivent être soumises à une contrainte plus grande pour pouvoir exister.

Maintenant que nous en savons plus sur l’énergie d’une dislocation essayons de voir pourquoi certaines réactions entre les dislocations sont attractives et d’autres répulsives. Considérons les dislocations de vecteur de Burgers $\vec{b}_1$, $\vec{b}_2$ et $\vec{b}_3$ telles que $\vec{b}_3=\vec{b}_1+\vec{b}_2$. Une réaction de jonction se poursuit que si il y a un gain d’énergie pour le système, c'est-à-dire si l’énergie de la dislocation $\vec{b}_3$ est inférieure à la somme de l’énergie des dislocations $\vec{b}_1$ et $\vec{b}_2$. Comme nous avons vu que l’énergie est proportionnelle à $\| \vec{b} \|^2$, on est conduit (en première approximation) à la condition suivante appelée critère de Franck :

$$\| \vec{b}_3 \|^2 \ge \| \vec{b}_1 \|^2+\| \vec{b}_2 \|^2$$

Dissociation

Inversement, on peut avoir une dissociation d’une dislocation en deux autres si le critère de Franck est satisfait. Nous allons voir un type de dissociation particulièrement intéressant dans les cristaux cubiques faces centrées.

Dans les cristaux cubiques faces centrées, les dislocations les plus stables sont celles qui ont une énergie la plus faible. Leur vecteur de Burgers, qui est une translation du réseau est alors : $1/2 a [110]$. Son énergie est donc proportionnelle à $a^2/2$. Si on représente ce type de cristal par un empilement ABC…, ce genre de vecteurs de Burgers correspond à une translation entre deux sites C laissant la structure invariante.

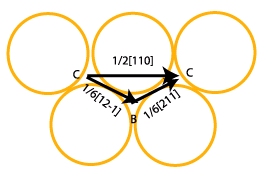
Je vous propose alors l’expérience suivante: fabriquons deux réseaux hexagonaux composés de balles de ping-pong collées les unes aux autres. Ils vont nous servir à représenter deux couches atomiques. Plaçons les balles de ping-pong de la seconde couche dans les sites C de la première. Essayons maintenant de déplacer les deux réseaux l’un sur l’autre dans une direction donnée. On s’aperçoit que les balles glissent plus facilement lorsque le mouvement s’effectue en deux temps comme représenté ci-dessous.

Ainsi pour effectuer une translation de type $a/2 [110]$, il est plus facile de faire deux translations de type $a/6 [12\bar{1}]$.

$$\frac{a}{2}[110] \rightarrow \frac{a}{6}[211] + \frac{a}{6}[12\bar{1}]$$

Si l’on écrit le bilan d’énergie, on voit clairement que cette opération représente un gain d’énergie : $a^2/2 > a^2/6+ a^2/6= a^2/3$. Les dislocations ainsi formées sont appelées dislocations partielles de Shockley. Si l’on se rappelle la représentation du tétraèdre de Thomson, les vecteurs de Burgers des dislocations de Shockley sont représentés par les vecteurs joignant les sommets aux centres des faces du tétraèdre.

Bien qu’énergétiquement favorable, encore faut-il que cette configuration soit stable. Il est aisé de voir que la force d’interaction entre les dislocations est répulsive car le produit scalaire entre les deux dislocations de Shockley est négatif.

Il y a quelque chose qui cloche pourtant. On a dit que les vecteurs de Burgers doivent être des translations du réseau, ce qui n’est pas pour des dislocations de Shockley. Observons ce qui se passe. Pour cela représentons un empilement caractéristique ABCABC, et imaginons que l’on déplace la partie supérieure du cristal d’une quantité égale au vecteur de Burgers d’une dislocation de Shockley :

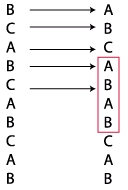
On remarque qu’un bouleversement dans l’ordre est apparu : on a créé une petite portion de cristal hexagonale ABAB… dans le cristal. On dit que l’on a créé une faute d’empilement. Ainsi, dans une structure cubique faces centrées, une faute d’empilement apparaît alors entre deux dislocations de Shockley.

Réexaminons maintenant le critère de Franck. Bien entendu, la formation d’une faute d’empilement coûte une énergie $\gamma$ par unité de surface. Les dislocations partielles sont alors soumises à la fois à une répulsion qui tend à les dissocier et une force de rappel due à la faute qui tend à diminuer l’énergie de surface de la faute $\gamma$. Un état d’équilibre est alors atteint lorsque ces deux forces se compensent. La distance d’équilibre est alors donnée par la relation :

$$d= \frac{\mu \left( \vec{b}_1 \cdot \vec{b}_2 \right)}{2 \pi \gamma}$$

Dans certains métaux et alliages l’énergie d’une faute d’empilement est tellement importante que les dislocations ne se dissocient pas ou peu (le critère de Franck ne s’applique plus).

Une autre dislocation partielle peut être créée si l’on considère la réaction suivante :

$$\frac{a}{6}[11\bar{2}] + \frac{a}{3}[111] \rightarrow \frac{a}{2}[110]$$

La dislocation de vecteur de Burgers de type $a/3 [111]$ est appelée dislocation partielle de Franck. On remarque immédiatement que cette dislocation est coin et sessile (non mobile) dans le plan de glissement $(111)$. On peut la concevoir comme le résultat de l’insertion ou du retrait d’une couche dans l’empilement ABC…

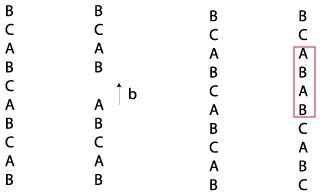
Ce genre de dislocation est généralement créé lors de l’irradiation dans une centrale nucléaire par exemple. En effet, dans ce processus fortement énergétique, des atomes de la structure peuvent être arrachés en créant un grand nombre de lacunes. Après un refroidissement rapide (on dit une trempe) à haute température, les lacunes ont tendance à coalescer en formant ainsi une boucle de Franck limitant la faute d’empilement.

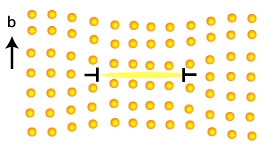
Comme ce type de dislocation est sessile, elle ne peut se déplacer que par montée, en absorbant (ou émettant) des lacunes. Nous avons vu que lorsque la contrainte est perpendiculaire au plan de la boucle et de même signe que $\vec{b}$, la boucle peut alors croître en absorbant des lacunes. Toutefois, la contrainte nécessaire doit être suffisante pour équilibrer à la fois la tension de ligne et la tension de surface due à la faute. Ce qui est intéressant d’observer c’est la croissance compétitive entre les boucles. Celles qui auront un diamètre supérieur à un diamètre critique vont continuer à croître au profit des plus petites qui en leur cédant des lacunes vont inexorablement disparaître sous l’effet de la tension de ligne. C’est un peu le même processus qui fait que les petites bulles de savon se vident dans les grosses, ce qui conduit alors à la disparition de la mousse !

Pour finir sur les fautes d’empilements, étudions ce qu’il advient lorsque plusieurs dislocations partielles glissent dans des plans parallèles voisins. Lorsque plusieurs dislocations laissent une faute d’empilement dans des plans voisins, ceci implique que la faute d’empilement est alors étendue non seulement dans le sillage des dislocations mais aussi dans la direction perpendiculaire au plan de glissement. On crée alors une lamelle qui est désorientée par rapport au reste du cristal. Ce phénomène c’est le maclage.

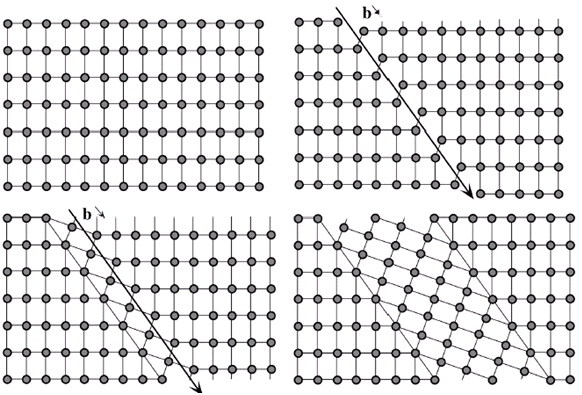
© J. Douin, Mécanique des milieux continus

Le processus de maclage s’accompagne d’une variation (faible) du volume du cristal. Dans le cas de l’étain, il s’accompagne même d’un petit craquement caractéristique appelé le « cri de l’étain ». Curieux non ?